The Expected Logarithm of a Noncentral Chi-Square Random Variable

In my Ph.D. thesis I have published a closed-form expression for the expected value of the logarithm of a noncentral chi-square random variable with even degrees of freedom. Recently I have now been able to generalize this to the expected value of the logarithm and also to negative integer moments of a noncentral chi-square random variable with arbitrary (i.e., even or odd) degrees of freedom. Moreover, I have found tight elementary upper and lower bounds to this expression.

Details can be found in

Stefan M. Moser: Expected Logarithm and Negative Integer Moments of a Noncentral χ^2-Distributed Random Variable, Entropy, vol. 22, no. 9, September 2020, art. no. 1048. (Abstract) [.pdf]

Keywords

Chi-square, chi-squared, negative moments, noncentral chi-square, noncentral chi-squared, expected logarithm, Rayleigh, Rice, Ricean, Rician.

Generalizations

The following lemma has been proven in (Appendix A, Lemma 3)

Angel Lozano, Antonia M. Tulino, Sergio Verdú: High-SNR Power Offset in Multiantenna Communication, IEEE Transactions on Information Theory, vol. 51, no. 12, pp. 4134–4151, December 2005.

Lemma: Consider an m times n random matrix h=hbar+w with m less or equal n , where hbar is deterministic while the entries of are zero-mean unit-variance IID complex Gaussian. Denoting by phi_j (j=1,...m) the eigenvalues of hbar hermi(hbar) we have

e[log det hbar hermi(hbar)]=...

where xi_i (i=1,...,m) is an m times m matrix with entries

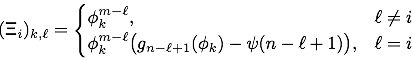
$(xi_i)_{k,l}=...$

-||-   _|_ _|_     /    __|__   Stefan M. Moser
[-]     --__|__   /__\    /__   Senior Scientist, ETH Zurich, Switzerland
_|_     -- --|-    _     /  /   Adjunct Professor, National Yang Ming Chiao Tung University, Taiwan
/ \     []  \|    |_|   / \/    Web: https://moser-isi.ethz.ch/

Last modified: Wed Sep 21 12:33:50 UTC 2022