My IT-Textbooks

The declaration of the copyright is at the bottom of this page. Please, don't hesitate to contact me at if you have any questions or if you need more information.

Information Theory (6th Edition)

I use these lecture notes in my course Information Theory, which is a graduate course in the first year. The notes intend to be an introduction to information theory covering the following topics:

  • Information-theoretic quantities for discrete random variables: entropy, mutual information, relative entropy, variational distance, entropy rate.
  • Data compression: coding theorem for discrete memoryless source, discrete stationary source, Markov source.
  • Lossless source coding: Shannon-type coding, Shannon coding, Fano coding, Huffman coding, Tunstall coding, arithmetic coding, Elias–Willems coding, Lempel–Ziv coding, and information-lossless finite state coding.
  • Karush–Kuhn–Tucker conditions.
  • Gambling and horse betting.
  • Data transmission: coding theorem for discrete memoryless channels, computing capacity.
  • Channel coding: convolutional codes, polar codes.
  • Joint source and channel coding: information transmission theorem, transmission above capacity.
  • Information-theoretic quantities for continuous random variables: differential entropy, mutual information, relative entropy.
  • Gaussian channel: channel coding theorem and joint source and channel coding theorem, average-power constraint.
  • Bandlimited channels, parallel Gaussian channels.
  • Asymptotic Equipartition Property (AEP) and weak typicality.
  • Short introduction to cryptography.
  • Review of Gaussian random variables, vectors, and processes.

Download current version: (new version 6.16)

To link to the most current version of these notes, use

https://moser-isi.ethz.ch/cgi-bin/request_script.cgi?script=it

These notes are still undergoing corrections and improvements. If you find typos, errors, or if you have any comments about these notes, I'd be very happy to hear them! Write to . Thanks!


Advanced Topics in Information Theory (5th Edition)

I use these lecture notes in my course Advanced Topics in Information Theory, which is an advanced graduate course. Based on the theory introduced in the introductory notes Information Theory, it continues to explore the most important results concerning data compression and reliable communication over a communication channel, including multiple-user communication and lossy compression schemes. The course covers the following topics:

  • Method of types.
  • Large deviation theory and Information Geometry. (New!)
  • Strong typicality.
  • Hypothesis testing, Chernoff–Stein Lemma.
  • Parameter estimation, Fisher information, Cramér–Rao Bound. (New!)
  • Guessing random variables.
  • Duality, capacity with costs, capacity with feedback.
  • Independence and causality: causal interpretations.
  • Error exponents for information transmission.
  • Context-tree weighting algorithm.
  • Rate distortion theory including error exponents.
  • Multiple description.
  • Rate distortion with side-information (Wyner–Ziv).
  • Distributed lossless data compression (Slepian–Wolf).
  • Soft covering. (New!)
  • Wiretap channel and secrecy capacity. (New!)
  • Multiple-access channel (MAC).
  • Transmission of correlated sources over a MAC.
  • Channels with noncausal side-information (Gel'fand–Pinsker).
  • Broadcast channel.
  • Multiple-access channel (MAC) with common message.
  • Discrete memoryless networks and cut-set bound.
  • Interference channel.

Download current version (new version 5.8):

To link to the most current version of these notes, use

https://moser-isi.ethz.ch/cgi-bin/request_script.cgi?script=atit

These notes are still undergoing corrections and improvements. If you find typos, errors, or if you have any comments about these notes, I'd be very happy to hear them! Write to . Thanks!


A Student's Guide to Coding and Information Theory

This textbook is thought to be an easy-to-read introduction to coding and information theory for students at the freshman level or for non-engineering major students. The required math background is minimal: simple calculus and probability theory on high-school level should be sufficient.

Link to Cambridge University Press:


List of Typos and Corrections:

  • On p. 15, in Footnote 1: Unfortunately, the way we have written the statement, it is not true. For a finite number of events 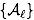{A_l} to be independent, one needs that for any subset of events it holds that

    independence of events

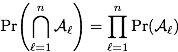
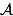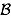    We should have focused on the case of two events only: two events A and B are independent if, and only if,

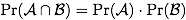
    independence of two events

  • On p. 89 in Lemma 5.10, the inequality only holds for b>1.
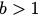  • Unfortunately, Lemma 5.22 (p. 99) does not hold. And it is not correct even if we replaced Eq. (5.68) by

    bound on Fano codeword length

    This then means that the derivation of the upper bound on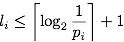 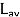L_av in (5.73)—(5.78) does not hold either. Nevertheless, the statement of (5.79) in Theorem 5.23 is true! It just turns out to be much more complicated to prove...
    (The interested reader can find more details to this issue in Chapter 4 of my lecture notes Information Theory, although I have not included the complete derivation yet, because I have only succeeded in proving it for binary and ternary codes and not in general. I hope that I will be able to fix this one day.)


Copyright

You are welcome to use the IT and ATIT lecture notes for yourself, for teaching, or for any other noncommercial purpose. If you use extracts from these lecture notes, please make sure that their origin is shown. The author assumes no liability or responsibility for any errors or omissions.


-||-   _|_ _|_     /    __|__   Stefan M. Moser
[-]     --__|__   /__\    /__   Senior Scientist, ETH Zurich, Switzerland
_|_     -- --|-    _     /  /   Adjunct Professor, National Yang Ming Chiao Tung University, Taiwan
/ \     []  \|    |_|   / \/    Web: https://moser-isi.ethz.ch/


Last modified: Thu Sep 5 13:39:51 UTC 2024